Any arbitrarily complex wave can be represented as a bunch of simple waves added together. By simple, I mean sine waves, which look like this:
Simply by adding together sine waves of different frequencies and amplitudes, you can recreate any waveform that follows standard equations rules, such as each x value having only one corresponding y value. The method of creating such a representation is called Fourier Analysis. By running an equation such as this:
you are able to create a graph of the dominant frequencies present in the original signal. The equation looks complicated, but it is essentially checking how much test sine wave, at any frequency analyzed in the range, matches with frequencies present in the original complex wave. The more the two waves match, the higher the value of the integral, and thus, the higher the peak on the frequency domain graph. This process can be run on the sounds of musical instruments, and through using simple oscilators at the correct frequencies, the sound of any instrument can be, roughly, recreated.
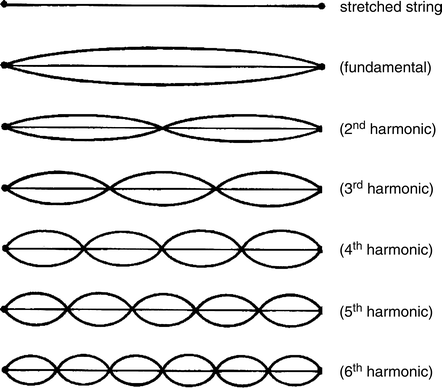
All tonal instruments vibrate in a very specific way. In the case of stringed instruments, a steady tone is produced when standing waves are established on the instrument. For a standing wave to reside on a string, it must have an integer number of evenly spaced nodes, or points of no vibration. This is because the ends of the string can't vibrate, meaning there will always be two nodes on either end of it. Since the addition of each node incurs an increase of one half of a wavelength, and the fundemental vibration, that with only two nodes, is half a wavelength, each subsequent mode will have a frequency n times greater than that of the fundemenal. Thus, if the fundemental vibration vibrates at 220 Hz (220 times per second), the second vibrational mode will happen at a rate of 440 Hz, and the one after that at 660 Hz, and so on.
*A note on increasing frequencies: Why does a shorter wave nececarily vibrate faster? All waves travel at a specific speed through a material, like the speed of sound in air. The equation:

relates the speed of the wave to its frequency and wavelength. Thus, if you decrease the wavelength of the wave by half, it's frequency has to double, with three times the wavelength, it has to triple, etc. Thus, every standing wave present on the string is traveling at the same speed across it, but since the wavelengths go down as you add nodes, the frequency of the subsequent vibrations goes up.
So if all stringed instruments have harmonics at integer multiples of the fundemental, what gives each instrument its unique sound? Due to the differing construction of each instrument, different harmonics are more or less emphasized. Thus, the relative amplitudes of the harmonics of a flute will differ from that of a banjo, even though both will have harmonics at the same frequencies, given that they play the same note.
I wanted to see if I could capture the essence of the sound of three instruments I have in my house: the violin, the bass guitar, and the piano, by recreating them using simple harmonic oscilators. Thus, I recorded samples of each instrument being played, where the string is either struck, as in the case of the piano (well, a recording of that, at least. It's an electric piano), or plucked, as in the case of the violin and bass guitar. I then created Fourier Power Spectrums for each recording, giving me the relative amplitudes of the harmonics present in each recording. Finally, I created a waveform using sine waves of the corresponding amplitudes and frequencies, added a decay to simulate a realistic sound, and exported them as sound files.

The instruments to be recreated.
First, here are the power spectrums for each of the three recordings:

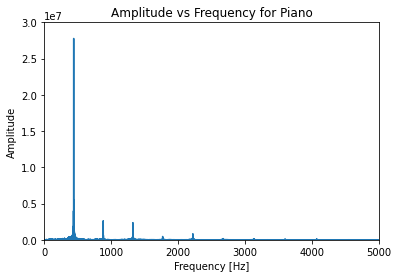
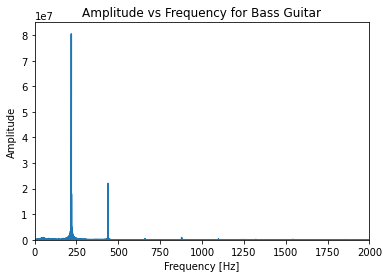
The violin has the most harmonic flavor present beyond the fundemental, and the bass the least, which makes sense, considering the way the two instruments sound.
And here are the original recordings versus my recreated versions:
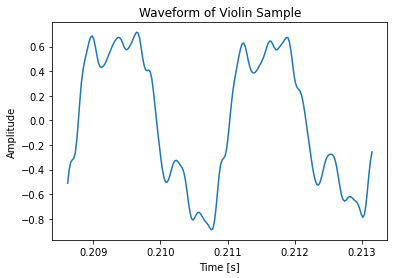
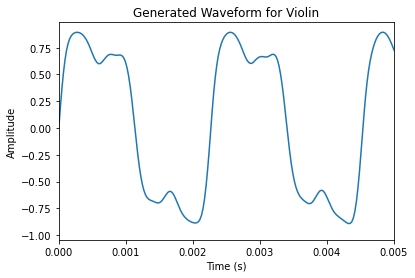
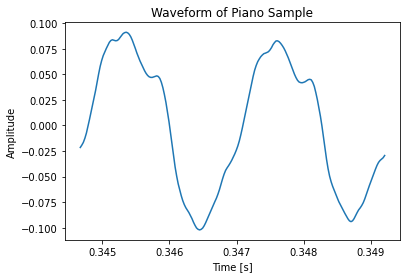
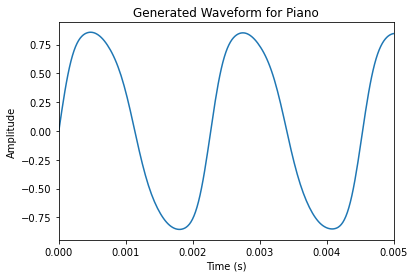
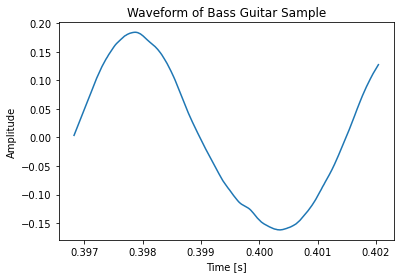
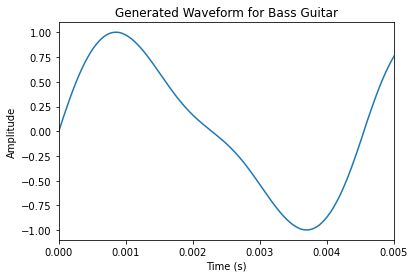
The bass sounds the most accurate, the violin sounds close, and the piano is perhaps missing a bit too much upper harmonic information, and sounds more like a simple sine wave. This discrepancy is likely because I sampled the full ringing of the note for the Fourier analysis. Higher frequencies decay on a string faster than lower ones, meaning on average more low-end harmonics exist on a recording than high-end ones. To get a more accurate sound, I could have perhaps only sampled the very beginning of each recording.
Finally, as a bonus, I was messing around with Fourier synthesis on Desmos, and came up with a crazy looking waveform, generated with the equation:
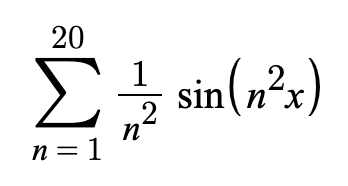
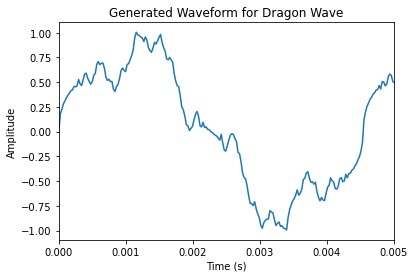
I nicknamed it the dragon wave because I thought it looked similar to the dragon curve, a type of fractal. It has the sound similar to that of a tubular bell. Here is its waveform and how it sounds, constructed the same way I constructed the previous three recreations.
As you can see, there is more nuance to the sound of a musical instrument than merely perfect harmonic vibrations. For example, subtle acoustic differences are imparted to the sound of a violin from the way the sound resonates in the hollow chamber inside it. However, by utilizing the this method, the rough timbre (musical word analogous to the math concept of Fourier analysis) of an instrument can be aproximated. Since timbre is the most important factor in determining the emotional effect of an instrument, it can be inferred that playing a song with my recreated sounds would achieve a similar emotional effect as that same song being played through real instruents.
Works Cited: Gunther L. (2012) The Vibrating String. In: The Physics of Music and Color. Springer, New York, NY.